Analyzing My Online Chess Games in R
“Fancy what a game of chess would be if all the chessmen had passions and intellects, more or less small and cunning; if you were not only uncertain about your adversary’s men, but a little uncertain also about your own.”
Overview
In trying to find a data source for a personal project, I realized I had a source I’d been unknowingly adding to everyday: my own online chess games. An intriguing question emerged as I brainstormed: what kind of findings can I pull out by analyzing chess notation?
The data for this analysis comes from Lichess, a popular online platform for playing chess, and includes notation for my games from June 2021 to November 2022 (a year and a half). This notation has the moves, date and time, player ratings, openings, time control, and results of each game. The file type is a “pgn” (portable game notation). As we’ll see, this format required quite a bit of clean up before we could analyze it.
This post covers the following areas in my analysis:
Research Questions & Key Findings
Data Cleaning & Variable Creation
Data Exploration & Insights
Predictive Modeling & Inferences
Note: if you’d like to check out my code, visit my GitHub repository.
Research Questions & Key Findings
After exploring the data, I identified several, more detailed research questions. I outline these below, as well as the main findings and inferences for each question. I used various capabilities within R, including data visualization (primarily using the ggplot2 package), statistical significance testing, correlation testing, and logistic regression.
Research Question 1: On which side of the board is my play most effective?
Findings: I win 53% of my games as white and 47% as black. This difference is statistically significant, meaning it’s likely not due to chance.
Inferences & Interpretation: This is not uncommon, since white starts the game with the first move and has an extra tempo.
Research Question 2: During which days of the week is my play most effective?
Findings: I win 52% of my games during the weekend and 49% during weekdays. This difference was not statistically significant. However, Thursday has the highest win percentage among all weekdays at 54%.
Inferences & Interpretation: I’m more likely to feel refreshed during weekends and therefore my play may be better during that time. However, Thursday’s win rate, and the lack of statistical significance in win rate between weekdays and weekends, shows that this may not always be true. I also noticed that the amount of games I play is more frequent during the weekend. I attribute my success on Thursday to the next day being Friday!
Research Question 3: Which openings may be over or under-utilized in my repertoire?
Findings: I play the Queen’s Gambit most often, but there are several more unusual openings which I play less and but with a higher win percentage. This includes the Nimzo-Larsen Attack (1. b3) as white and the Scandinavian Defense as Black (1. e4 d5).
Inferences & Interpretation: Playing lesser-known openings may be worth exploration as an element of surprise in games. However, I’d caution that shorter time formats and opponent skill level are factors here which should be taken into consideration. Regardless, there’s certainly an opportunity to incorporate some offbeat play in the opening choice.
Research Question 3: How does the frequency of major and minor piece moves (the Bishop, Knight, Rook and Queen) as well as the King, differ between wins and losses?
Findings: Major and minor piece moves, as well as the number of checks, are more frequent in wins. King moves are more frequent in losses. Differences in piece moves (including checks) between wins and losses were statistically significant except for the King. Interestingly, the Bishop had the highest number of average moves in wins.
Inferences & Interpretation: Higher frequency of major and minor piece moves may be a product of more effective development and piece activity, common principles in creating an advantageous position. The Bishop having the highest number of average moves in wins is important: while piece value is dependent on the position, it’s often said the Bishop has slightly more than its counterpart, the Knight. More frequent King moves in losses are probably correlated with more frequent checks in wins. Both are likely due to combinations which are attempting to go after the opponent’s King and checkmate them.
Research Question 4: How common are repeated results (the current game’s result was the same as the last’s)? Are winning streaks or losing streaks more common?
Findings: 47% of all games are repeated results; 25% of these repeated results were wins while 22% were losses. Among winning games, 51% are repeated results while 47% of losses are repeated results. This difference was statistically significant.
Inferences & Interpretation: The prevalence of repeated results could be a sign of the patterns we fall into: when we’re winning, the confidence builds up and it can carry over to the next game. When we’re losing, it can be hard to get out of a slump. However, the higher prevalence of winning streaks could mean that the confidence from winning a game has a stronger effect than the dismay from losing.
Research Question 5: Can we make a relatively accurate model to predict winning a game based on chess notation?
Findings: I created a logistic regression model to predict whether or not a game was won, which had a 66% accuracy on the train set and 64% on the test set.
Inferences & Interpretations: Ideally, the accuracy should be higher. However, with no baseline for comparison, it’s hard to know if a higher target range is reasonable. The available (or potential) variables in chess notation may not be sufficient to create a model with a higher accuracy. Or maybe it is and there’s further research to be done.
Research Question 6: Which inferences can we make about the prediction power of variables within chess notation on the odds of winning a game?
Findings: As a category of variables, moves of my major and minor pieces had the highest number of significant predictors on the odds of winning a game, ranging from an increase of 4% - 10% with each additional move (except for the King, which had -6.6%). However, the strongest predictor was whether or not a game was in the Rated Rapid format (between 10 to 15 minutes each with the possibility of an increment). This increased the odds of winning by 339%. Playing during a weekday had the most negative effect on the odds of winning (-24.7%).
Inferences & Interpretation: While the model didn’t have the desired accuracy, many of these findings felt congruent with my own experience and other findings in the analysis. I play much better and have had a higher sustained rating in the longer, Rapid time format (though I’ve played far less games). The more incremental positive or negative changes in odds based on piece activity agrees with prior insights. As a next step, it’d be interesting to do a factor analysis among these variables to identify and quantify their underlying factors.
Before proceeding, please note that this post includes a fair amount of detail on the full process I went through for each step from this point forward, including screenshots of my code, output and explanations.
Data Cleaning & Variable Creation
First, I load in the dplyr and stringr libraries for some initial transformations to clean the data, then read in and review the file using the View function. Note that I’ll be hiding the usernames of my opponents and myself as well as the URLs of the games for privacy.
The main areas I concentrated on first in cleaning are removal of unnecessary words, characters and rows which may not be needed for the analysis. We also want to turn the rows into columns so we can build out the data frame and explore specific variables. I also include a reverse ID column since the games were read into RStudio in reverse chronological order. This will come in handy when examining trends over time later.
Now let’s use the skim function to review the data frame.
We’re looking at a total of 2,630 games and 15 variables (14 characters and one numeric). We’ll convert those variables to the correct classes and clean them accordingly. We can also see that there are no missing values. Let’s move onto cleaning the individual columns and trying to extract new variables from them which may be valuable to the analysis.
First, I focus on the Game_Type column. After using the table function, it’s clear that “Rated Blitz” is the most frequent category, making up 76% of my games. This variable will be important when analyzing my rating, since the blitz, rapid and bullet formats each have their own ratings. I can also see that there are some unnecessary words in these values we can remove. Lastly, let’s convert this variable to a factor and create new columns with binary indicators for each game type, a 1 indicating that a specific game type was played and a 0 indicating that it was not. This will be useful for our model later.
Let’s see what our new columns look like.
Next, let’s clean the Date column. After again removing some unnecessary words, I convert the variable to a Date type and extract both days of week and month and year as new columns.
The Opening column includes both the general category of the opening (for example: The French Defense) as well as the variation (for example: Steinitz Attack). So that I can examine both categories, I create two new columns: Opening_Type and Opening_Variation. All Opening columns are then converted to factors. The first of these two new sub-categories will help us get a more high-level view of my opening repertoire, while the second can help with more granular research.
See below how this effectively splits the openings into their general categories and variations.
Next, I created new columns to show whether I played as black or white using an if_else statement within the mutate function then created columns to show my results, both overall and as each side of the board. The “I_Win” variable I created is a binary indicator showing if I won or not (1 means I did win, 0 means I didn’t). This would be the response variable in the logistic regression model.
Now we have various columns to use for our analysis to better understand not just insights for winning games, but winning games as white or black and losses and draws as white or black. This also gives us the flexibility to choose either categorical or binary variables to explore these areas. See below the range of variables we now have to explore in relation to result and side of the board.
One of the trickiest parts of the data cleaning process was the creation of columns to show the number of moves in each game and the number of moves of each minor and major piece as well as the King. Each move in chess notation (example: 1. e4 c5 …) has three spaces. Therefore, we can count the number of spaces in the Moves column and divide by three to arrive at the total. However, what if the game ends with a move by white (example: 30. Qd8 ##)? Then, we have two spaces. To account for this, we use the “ceiling” function, which rounds up to the nearest whole number.
Next, how do we extract the number of moves of each piece (excluding pawns)? Note that each move by white begins with a number, period, then space followed by the move (example: 1. e4). We can simply count the number of strings with this pattern to arrive at the total number of moves for white. But what about black? We can get this by subtracting white’s moves for each piece from the total number of moves of each piece from the game. I can then use previously created columns indicating which side I played to show if they were my moves or my opponents’.
Now we have columns to show the number of moves of each game and the number of times my opponent and myself moved each piece, all of which will play key roles later in the analysis.
Using some of the same methodology, I also created columns to show the number of checks in total, for both sides of the board and myself. I wanted to see if this could be a strong variable in predicting the probability of a win, which I’d explore later when training the model. A higher number of checks could mean that an opponent’s king is in trouble.
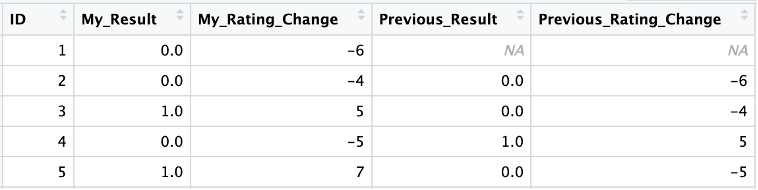
Lastly, I also created variables to show rating differences between myself and my opponent as well as the result and rating changes from the previous game. I wanted to see if any of these may have an impact on results, but also how common winning and losing streaks are. This is where the backwards ID column comes in handy. First, I sort the games from earliest to most recent using the ID, then I create two new variables using the lag function: one showing the result of the last game (win, loss or draw) and one showing the rating change resulting from that game.
Note that this created NA values for the first game since there’s none preceding it in the data set. We’ll need to account for this later in the analysis.
Let’s take a step back and look at our data frame now using the skim function below.
We have 98 variables in total compared to the 15 we started with. Please note that I did not cover all steps of cleaning and variable creation in this written summary, only the most illustrative and key areas.
Looking further down the skim summary, there were no NA or missing variables except for the Previous_Result, Previous_Rating Change and Opening_Variation columns. These were not necessary to impute or modify at this stage of the analysis.
Data Exploration & Insights
Now let’s dive into the data and start exploring those research questions.
On which side of the board is my play most effective?
Typically, playing white gives an advantage because you move first and start with an extra tempo. I discovered that, as white I win 52.8% of my games, while as black, I win 47% of my games.
There’s a difference in win percentages by 5.7, but is it significant? Rather, is my higher win percentage as white due to chance, or are we likely to see the same level of difference or more extreme in other games of mine?
I explored this question by using a two-sample test of proportions. The null hypothesis here is that playing as white or black makes no difference in the percentage of won games (the proportions are equal), while the alternative hypothesis is that playing white or black does create a difference in win percentage (the proportions are not equal). I create several values then plug them into the prop.test function to arrive at the answer.
Based on the p-value being below a 95% confidence level (or alpha of 0.05), we can conclude that the difference is statistically significant. More specifically, the p-value tells us that, under the null hypothesis (the scenario where we assume playing white or black creates no difference in win percentage), we have a 0.3% chance of seeing this same level of difference or more extreme in out-of-sample data. This low percentage therefore allows us to reject the null hypothesis. In other words: there’s a high likelihood that I tend to win more as white in general, outside of the games used in this analysis.
Which openings do I play most frequently and are any over or under-utilized in my repertoire?
As a “1. d4” player (meaning I tend to start games as white by moving my queen pawn two spaces), I have a relatively good idea of which openings I tend to play the most as white. However, I want to better understand how much variety (or lack thereof) my repertoire has and other openings I may want to explore. I used the ggplot2 library to help with visualizations in exploring this question.
First, let’s see which openings I play most frequently as white.
Not surprisingly, I have a high tendency to play Queen’s Gambit games. The first three most frequent openings (Queen’s Gambit Declined, Semi-Slav Defense and Slav Defense) are all variations of the Queen’s Gambit. These three openings make up about 22% of my overall games and 43% of my games as white.
But how do I perform in each of them and which openings should be further utilized? To answer this question, I used a scatter plot, plotting the same openings by their frequency vs. win percentage. Note here that I made the color of the points “white” to have more focus on the labels. The ggrepel package was also very handy here in avoiding overlapping text.
Queen’s Gambit openings are clearly more frequent and I have relatively solid performance in them, winning between 55% - 58% or so of the games. However, I’m interested in the upper-left quadrant: games played less frequently with a higher win percentage. Specifically, the Nimzo-Larsen Attack stands out here. While I’ve only played 28 games with this opening, it has the highest win percentage at 61%. Recently, to mix up my opening choice, I’ve been briefly studying and playing this opening. The Nimzo-Larsen Attack is considered a more unusual opening, where white tries to take control of the center indirectly through a “flank” approach by fianchettoing the Queen bishop.
Now let’s look at the same insights for black. As shown in the charts below, the Sicilian (1. e4 c5) and Scandinavian (1. e4 d5) openings are most common (my main replies to 1. e4). However, as shown in the scatter chart, I win slightly more games with the Scandinavian.
During which days of the week is my play most effective?
To look at performance by day, I first created a data frame that grouped the total number of games by day. I then used an inner join to this data frame, combined with a mutate function, to create a stacked bar chart showing my results throughout the week.
Note how both Saturday and Sunday have just over 50% in wins, while weekdays (excluding Thursday) are below that. Let’s create new variables from this showing whether a game took place on a weekday or weekend. To do this, I first created binary indicator columns.
Now let’s compare performance between the two.
I win 52% of my games during the weekends and 49% during weekdays. In aggregate, this doesn’t seem like a big difference. But like the exploration of performance based on side of the board, let’s see if this difference is statistically significant.
If we again assume a confidence level of 95% (or alpha of 0.05), the p-value from the two-sample test of proportions indicates that this difference is not statistically significant and may be due to chance. Under the null hypothesis (a scenario where we assume there is no difference in win percentage during weekdays vs. weekends), we have a 21.9% chance of seeing this same difference in out-of-sample data. Therefore, we cannot reject the null hypothesis and conclude a true difference.
How does the frequency of major and minor piece moves, as well as King moves, differ between wins and losses?
I’m interested to see if both the major (Queen and Rook) and minor (Knight and Bishop) pieces tend to move more frequently in wins, and if the King moves are more infrequent. This may be an indication that more active play with the major and minor pieces is associated with better development and better winning chances, while a more active king could be a sign that it’s in danger.
I take quite a few steps here to prepare the data for visualization to explore this question. First, I create a new “long” form of data with piece moves by wins and losses, replace strings with more conventional names, convert the piece moves to an ordered factor (purely for ordering along the x-axis), then translate this to a graph with multiple box plots.
The inner-quartile ranges for pieces moves in wins is more extensive than those for losses, except for the King. In addition, as indicated by the blue dots, the averages of major and minor piece moves tend to be higher as well for wins. This aligns with my previously mentioned guess at which piece moves may be more frequent or infrequent in wins vs. losses. However, there are many possible takeaways here, none of which can be definitive based on this data alone. But again, let’s see if this difference is statistically significant or due to chance.
I did a two-sample t-test to answer this question, comparing the average moves for each piece in wins vs. losses. In this test, the null hypothesis is that there is no difference in average piece moves between wins and losses (the difference is zero), while the alternative hypothesis is that there is a difference (the difference is not zero). Let’s see what these tests produced:
All major and minor pieces have significantly higher average moves in wins than losses, while the King has a non-significantly lower average of moves. This further substantiates my hypothesis that major and minor pieces move more frequently in wins but there’s insufficient support here of my hypothesis about more frequent king moves in losses. Note that there’s a caveat here: in this test the piece moves are the dependent variable while the independent variable is the outcome of the game (win or loss). Throughout this analysis, the game outcome has typically been the dependent variable. However, in this test, I propose that the piece moves respond to the qualities of a won or lost game, which may include more time and space for their development (or lack thereof).
How common are repeated results (the current game’s result was the same as the last’s)? Are winning streaks or losing streaks more common?
My hypothesis here is that the result of a previous game (win, loss or draw) has a relationship with the result of the next game. Specifically, I believe winning streaks (which we’ll define as winning more than one game in a row) are more common than losing streaks (losing more than one game in a row). Let’s do some comparisons to check this hypothesis.
First, we’ll calculate the total percentage of games which have repeated results, repeated wins and repeated losses.
Repeated wins are more frequent than repeated losses by three percentage points. Now let’s see how frequent repeat wins are among winning games and repeat losses among losing games.
Essentially: 51% of wins were preceded by a win, while 47% of losses were preceded by a loss. My hypothesis here seems to check out, but let’s do some testing here to dig further.
Let’s assume that our independent variable here is whether a game was won or lost, while the dependent variable is a repeated result. As shown in the two-sample test of proportions below, we can see that the difference in repeated results between won or lost games is statistically significant.
Predictive Modeling & Inferences
Based on the variables created so far, I tried to create a model predicting whether or not a game was won. This proved to be fairly difficult in terms of getting a relatively strong accuracy. The highest accuracy I got was 66% using logistic regression. My conclusions from this were the following:
There are still more valuable variables to extract from the data that can inform the likelihood of winning.
The data may not capture information sufficient to predict a winning result. Elements like timestamps or positional evaluations from Lichess for each move would likely help.
While these aspects are available in the platform, I wanted to see if it was possible to generate 70% accuracy or higher with just the notation. Regardless, we glean some informative insights from this process about variables that might be important to understanding the odds of winning a game (the proportion of wins vs. losses and draws).
Feature Selection
First, I create a new data frame with the features of interest I want to include in my model training. The selection of these features is based on the data exploration thus far and my own domain knowledge.
Next, let’s split the data into train and test sets. We’ll train our model on the “train” data, identify accuracy, then see if the results are consistent with the “test” data.
Before diving into training our model, let’s identify any sources of collinearity which may throw off our results. To do this, I like using the cor_test function from the rstatix package. This easily allows you to look at bivariate correlations across specified variables of a data frame, as well as the p-values to see if the relationship is significant. Depending on the amount of variables you’re correlating however, using this function can be somewhat computationally intensive.
Note here that the condition in the filter function ensures that we omit correlations of variables with themselves. Let’s take a look at the correlation data frame.
So what’s the point of creating this data frame? First, let’s take a look at the variables which have a statistically significant correlation with the “I_Win” variable. Assuming there may be a linear relationship in the data, this could help us identify potential predictors for our model.
While there are a handful of variables that have a significant relationship with the response variable, the strength of correlation is relatively week (all between 0.2 and -0.2). What does this mean? There is an association between these variables, it’s just not very strong.
Next, let’s try to identify sources of possible collinearity to eliminate before training the model. To do this, we’ll drill down to strong correlations (0.7 or greater or less than -0.7) between variables. I first filter this data frame to correlations which have an absolute value of 0.7 or greater, deduplicate rows with the same statistic value (as these are highly unique) to remove instances of repeated relationships, then arrange the relationships in descending order based on the correlation value.
Let’s see what we get.
Most of these are not surprises, such as Played_White and Played_Black as well as Weekend and Weekday being perfectly correlated. But how should we go about the process of elimination and selection? For variables that are perfectly correlated, I’ll make the more common variable in the data set the reference. For variables that are not perfectly correlated, I’ll choose the one which has a higher correlation with the “I_Win” variable.
After finalizing the variables in my training data, I try out several algorithms to predict accuracy of winning a given game. In creating the models, my primary purpose was to make inferences about which variables may be the strongest predictors.
Logistic Regression
In creating the logistic regression model, I compared my predicted vs. actual results and decided on a cut-off value of 0.5 probability (equal to or higher than this would be a win, lower than this would be a non-win).
Let’s take a look at the first ten results. Note that the “Correct” column indicates whether or not my prediction was correct.
5/10 are correct. As it turned out, this wasn’t too far from the model’s accuracy, which was 66% for the train data and 64% for the test data. Ideally, an accuracy above 70% or 80% would have been more desirable. However, without a baseline for predicting results using this type of data (frequency of piece moves, previous result, side of the board, etc.), it’s hard to know if that target range is feasible. Regardless, while directional, we can extract some interesting learnings from our model. To that end, let’s look at the summary of our logistic regression model.
From this, there are several, directional inferences we can make. Below, I’ve listed the variables which have a statistically significant, non-zero relationship with winning a game (grouped by categories), along with their effect on the odds expressed as a percentage. To calculate these figures, I subtracted one from the exponentiated coefficients of the logistic regression model.
For the binary variables (such as Weekday), we can interpret these percentages as: the percentage change in the odds of winning a game when the value is true compared to when it’s not. As an example: The odds of winning a game decreases by 24.7% during weekdays.
For the discreet variables (such as My_Queen_Moves), we can interpret these percentages as: the percentage change in odds of winning a game when the variable increases by a unit of one. Again, as an example: For every move my Queen makes, the odds of winning a game increases by 9.5%.
Some inferences we can make from these results:
As a category, my piece moves (and checks) have the highest number of significant predictors on the odds of winning on a game. Specifically, the number of checks has the strongest effect within this category. Each check increases the odds of winning by 11.7%.
Playing Rated Rapid games is the strongest predictor of the odds of winning a game overall. Anecdotally, this makes sense. I play much better in the Rapid time format (10 minutes each side, specifically) than Blitz on Lichess. I won 54% of my games in Rapid vs. 50% in Blitz.
Playing during weekdays has the most negative effect on the odds of winning games (based on its lowest odds ratio value).
Conclusion
Let’s go back to the original seed question which started this analysis: what kind of findings can I pull out by analyzing chess notation? Based on this exploration, notation is full of potential for extracting new variables and trying to identify the components of a winning game. While it may not be sufficient to create a model with high accuracy, it allowed me to quantify the patterns in my play and recognize their congruence with common principles and characteristics of the game.
As mentioned earlier, I believe this analysis may benefit from other variables such as position evaluations and timestamps for each move. However, it was an interesting experiment to see what types of insights we could glean from what started as more lean and unstructured ingredients. Specifically, I believe the insights on repeated results and move frequency by pieces were some of the most intriguing areas worth further exploration to see how they may vary or agree in relation to other players with different skill levels.